Comment sait-on que l’univers est en expansion ?

Jacques Treiner, Université Paris Cité

Commençons par une petite expérience qui va nous donner une image d’un « univers en expansion ». Cet univers sera un ballon gonflable.

On marque avec un stylo un point quelconque sur la surface et on trace un petit cercle autour, en marquant deux points sur le cercle. On gonfle le ballon progressivement.

À mesure que le cercle grandit, la distance au centre grandit, de même que la distance entre les deux points du cercle. Cela s’applique quel que soit le point initial choisi. Pour avoir une image d’un univers en expansion, il suffit de généraliser le cas d’une surface au cas d’un volume. Chaque point « voit » les autres points s’éloigner de lui comme s’il était le centre de l’expansion.

Une expansion à grande échelle, mais pas forcément locale

Il faut à présent expliquer comment les scientifiques en sont venus à cette conclusion en ce qui concerne l’univers observable, et pas seulement un ballon gonflable.

Pour cela, il faut observer l’univers à grande échelle. Ni la Lune ni le Soleil ne s’éloignent de la Terre, pas plus que les autres objets du système solaire. Les étoiles de notre galaxie, la Voie lactée, ne s’éloignent pas de nous. Et même la galaxie d’Andromède, qui se trouve à plus de deux millions d’années-lumière (AL) ne s’éloigne pas de nous. Au contraire, elle se rapproche de nous à une vitesse de 500 km par seconde.

L’univers est-il vraiment en expansion ? Oui, mais à des échelles de dizaines, de centaines de millions et de milliards d’AL. En moyenne, les galaxies s’éloignent les unes des autres, mais cela n’empêche pas que localement certaines se rapprochent, et même entrent en collision.

Nous connaissons l’expansion de l’univers depuis les années 1920, époque à laquelle les astronomes (américains, en l’occurrence) ont observé que les objets célestes lointains s’éloignaient de nous, et que leur vitesse d’éloignement était d’autant plus grande qu’ils étaient éloignés. Pour cela, il fallait être capables de mesurer, pour chaque objet, sa distance à nous et sa vitesse.

[Près de 70 000 lecteurs font confiance à la newsletter de The Conversation pour mieux comprendre les grands enjeux du monde. Abonnez-vous aujourd’hui]

Mesure des vitesses

Le déclic vint lorsque les physiciens analysèrent la lumière venant des étoiles, à commencer par le Soleil. Newton comprit que la lumière blanche était composée d’un continuum de longueurs d’onde, mais ce n’est qu’au début du XIX^e siècle que Frauenhoffer, un physicien allemand, remarqua la présence de lignes sombres dans le spectre solaire.

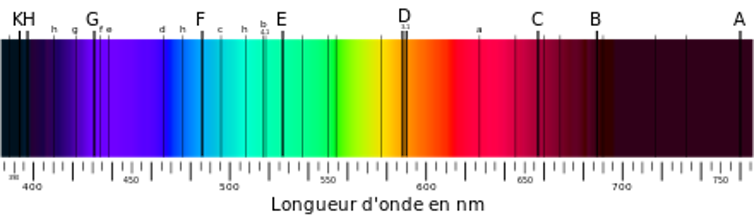
Ces longueurs d’onde « absentes » sont dues à leur absorption par les éléments présents à la surface de l’étoile, qui les diffusent ensuite dans toutes les directions, ce qui se traduit par un assombrissement dans la ligne de visée. Un ensemble de lignes sombres caractéristiques indique la présence d’un élément chimique.

Encore un siècle plus tard, des astronomes remarquèrent, dans le spectre d’étoiles appartenant à des galaxies lointaines, que ces ensembles de lignes sombres avaient tous, en moyenne, un décalage vers les grandes longueurs d’onde par rapport à ce que l’on observe en laboratoire, donc un décalage « vers le rouge ».

Ils interprétèrent ces décalages comme un effet Doppler lumineux, phénomène qui se produit lorsqu’une onde (acoustique ou lumineuse) est émise par une source en mouvement par rapport à un récepteur.

La longueur d’onde perçue se décale vers les courtes longueurs d’onde lorsque la source se rapproche du récepteur et vers les grandes longueurs d’onde lorsqu’elle s’en s’éloigne. L’effet augmente à mesure que la vitesse de la source émettrice augmente. On peut observer ce phénomène lorsqu’une ambulance passe devant nous, la sirène étant plus aiguë ou plus grave selon que l’ambulance se rapproche ou s’éloigne de nous. Ces décalages « vers le rouge » signalaient donc que les étoiles émettrices appartenaient à des galaxies s’éloignant de la nôtre. Il fallait encore déterminer si ces décalages étaient corrélés aux distances des sources émettrices. Ce n’est qu’au début du XX^e siècle que les astronomes disposèrent de l’outil permettant de mesurer ces distances.

Mesure des distances

Pour des étoiles distantes de quelques années-lumière, on utilise la méthode de la parallaxe orbitale. Si l’on regarde une étoile à six mois d’intervalle, sa position par rapport au fond du ciel change. On appelle parallaxe l’angle sous lequel on voit la distance Terre-Soleil depuis l’étoile. Cet angle est égal à la moitié du changement de la ligne de visée vers l’étoile à six mois d’intervalle.

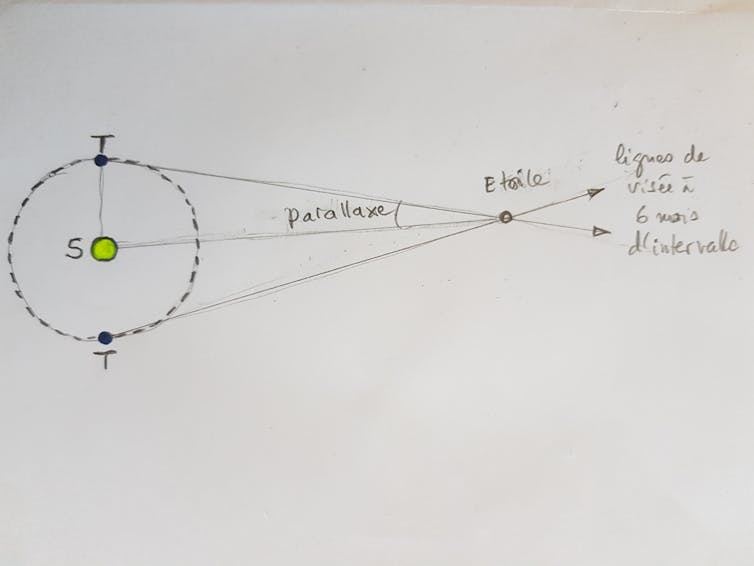
Mais cette méthode ne convient pas pour des étoiles ou des galaxies lointaines, car la parallaxe est trop petite pour être mesurée, la distance Terre-Soleil étant relativement trop petite.

La solution fut trouvée en 1908 à Harvard, où une jeune astronome, Henrietta Swan Leavitt, mesurait l’éclat d’étoiles appartenant à une nébuleuse visible dans l’hémisphère sud, le Petit Nuage de Magellan (M). En ce début de siècle, les progrès de l’instrumentation – télescopes et photographie – permirent de constituer les premiers grands catalogues d’étoiles.

À Harvard, les photos prises par les astronomes (essentiellement des hommes) étaient analysées par une équipe d’une douzaine de femmes, et Henrietta Leavitt s’intéressait aux étoiles variables, les Céphéides, appelées ainsi parce que la première fut découverte (en 1784) dans la constellation Céphée. Ce sont des étoiles géantes dont l’éclat varie avec une périodicité allant de l’ordre de la journée à quelques mois.

Leavitt découvrit une relation entre la période d’une étoile et sa luminosité. Plus elle est lumineuse, plus sa période est grande. Comme elles appartiennent toutes au même groupement d’étoiles, on peut considérer qu’elles sont toutes à peu près à la même distance de la Terre, d(M), si bien que les différences de luminosité reflètent leurs différences d’éclat intrinsèque.

Imaginons alors que l’on repère une Céphéide dans une autre galaxie. On mesure sa période P et on la compare avec celles des Céphéides du Nuage de Magellan. Cela permet de déterminer la luminosité L(M) qu’elle aurait si elle se trouvait à la distance d(M). Or la luminosité apparente Lap diminue comme le carré de la distance : Lap = L(M)〖d(M)〗²/d². Connaissant la distance du Nuage de Magellan, on en déduit la distance d de la Céphéide.

On peut aussi calibrer la relation période-distance en mesurant la période de Céphéides de notre galaxie, dont on connait la distance par mesure de parallaxe, et l’utiliser pour déterminer la distance du Petit Nuage de Magellan.

En tout cas, on tenait là l’outil recherché. De la mesure de la période d’une Céphéide, on pouvait déduire sa distance.

L’univers est bien en expansion

Au début du XX^e siècle, la question de savoir si tous les objets célestes visibles appartiennent à notre galaxie ou s’il existe d’autres galaxies séparées de la nôtre était débattue. C’est la mesure des distances décrites ci-dessus qui trancha le débat, la Voie lactée devint une galaxie parmi d’autres.

Mais c’est aussi la méthode qui permit à l’astronome américain Edwin Hubble de mettre en évidence l’expansion de l’univers. Il s’aperçut en effet qu’il existait une corrélation entre la vitesse d’éloignement d’une galaxie et sa distance. Plus une galaxie est lointaine, plus sa vitesse d’éloignement est grande.

On caractérise cette expansion par la « constante de Hubble H0 », qui indique de combien la vitesse augmente lorsque la distance augmente d’un million de parsecs (Mpc), distance équivalente à 3,2 millions d’AL. Actuellement, lorsque l’on s’éloigne d’un mégaparsec, la vitesse des objets célestes augmente de 74 km/s.

Conséquence immédiate : si l’on remonte le cours du temps, l’univers se contracte, sa densité augmente. Jusqu’où ? Bonne question, mais c’est un autre sujet, celui du Big-Bang !

Jacques Treiner, Physicien théoricien, Université Paris Cité